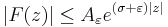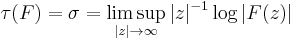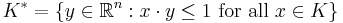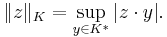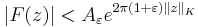Exponential type
In complex analysis, a branch of mathematics, an entire function function 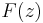 is said to be of exponential type
is said to be of exponential type  if for every
if for every  there exists a constant
there exists a constant 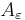 such that
such that
for every 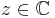 . We say
. We say 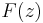 is of exponential type if
is of exponential type if 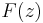 is of exponential type
is of exponential type  for some
for some 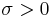 . The number
. The number
is the exponential type of 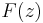 .
.
Exponential type with respect to a symmetric convex body
Stein (1957) has given a generalization of exponential type for entire functions of several complex variables. Suppose  is a convex, compact, and symmetric subset of
is a convex, compact, and symmetric subset of 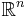 . It is known that for every such
. It is known that for every such  there is an associated norm
there is an associated norm 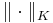 with the property that
with the property that
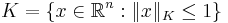 .
.
In other words,  is the unit ball in
is the unit ball in 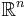 with respect to
with respect to 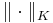 . The set
. The set
is called the polar set and is also a convex, compact, and symmetric subset of 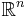 . Furthermore, we can write
. Furthermore, we can write
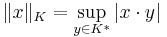 .
.
We extend 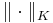 from
from 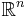 to
to 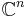 by
by
An entire function 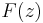 of
of  -complex variables is said to be of exponential type with respect to
-complex variables is said to be of exponential type with respect to  if for every
if for every 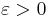 there exists a constant
there exists a constant 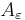 such that
such that
for all 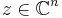 .
.
See also
- Paley–Wiener theorem
- Paley–Wiener space
References
- Stein, E.M. (1957), "Functions of exponential type", Ann. of Math. (2) 65: 582–592, JSTOR 1970066, MR0085342